What Is Sensitivity and Why Are Sensitivity Statements Often Misleading#
The response curve for a light sensitive sensor can be divided into three parts: the dark area, the linear area, and the saturation area.
A typical response curve is shown in the graph below.
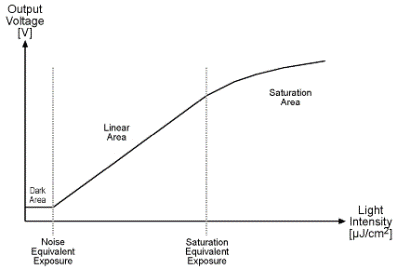
The dark area of the response curve shows the sensor's response to very low light. The output of the sensor in the dark area is very low, is noisy and is unpredictable. As you gradually increase the light falling on a sensor, you will find a point where the output of the sensor begins to increase predictably as the amount of light increases. This point is called the Noise Equivalent Exposure (NEE).
After the NEE point is reached, the output of the sensor becomes linear. The output remains linear until a point called the Saturation Equivalent Exposure (SEE) is reached. At this point, increasing the light intensity results in a nonlinear increase in the sensor output.
The gradient of the linear portion of the sensor's response curve is commonly referred to as sensitivity and is usually measured in V/µJ/cm². The higher a sensor's output voltage is for a given amount of light, the higher its sensitivity.
But sensor quality is not just about sensitivity. The NEE point is also very important. Since a sensor with a high NEE will be "blind" at low light levels, the NEE should be as low as possible.
Another point to consider is that a digital camera is a system and that sensor sensitivity is just one of the factors involved in the output signal from the camera. Electronic devices in the camera such as analog to digital converters and amplifiers also influence the output signal.
At Basler, we feel that a camera's "responsivity" is a better measure of camera performance. We also think that since our cameras are digital, responsivity should be stated as DN/µJ/cm² (DN stands for digital number). The graph below shows a responsivity curve.
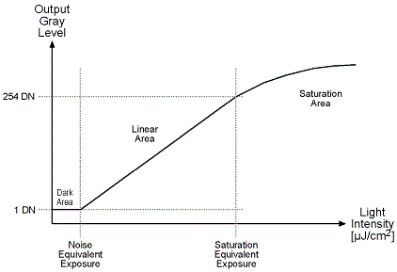
If a camera provides a gain feature, as most of them do, responsivity will depend on the gain setting.
And responsivity really only makes sense when it is stated in combination with a measurement of the camera's noise such as peak-to-peak, signal-to-noise ratio.
Let's consider an example. Suppose that you are comparing two cameras and that they have the following specifications:
Camera one:
- Responsivity = 1 DN/µJ/cm²
- Noise = 2 DN (peak-to-peak)
Camera two:
- Responsivity = 2 DN/µJ/cm²
- Noise = 5 DN (peak-to-peak)
At the first glance, camera two seems better than camera one because its responsivity is higher. However, if camera one has a gain feature, we can adjust the gain and increase the responsivity to two. Keep in mind that if we adjust the gain to double the responsivity from one to two, we will also double the noise. Now we have this situation:
Camera One:
- Responsivity = 2 DN/µJ/cm²
- Noise = 4 DN (peak-to-peak)
Camera Two:
- Responsivity = 2 DN/µJ/cm²
- Noise = 5 DN (peak-to-peak)
Which camera is better? They now both have the same responsivity, but camera one has lower noise. Camera one would be the better choice.
The lesson to be learned from all of this is that sensor sensitivity alone does not tell the entire story, and that we should be sure to use similar measuring criteria when we are comparing cameras.