Operator Library: Memory
The operator implements an approximation of a look up table through a set of base points. Thus the name KneeLUT. The range of all representable values on the operator output is divided by Knee LUT into N intervals defined by the base points. The amount of intervals N is representable as a number of power of 2, i.e. N = 2^n, n is an integer number. Parameter BasePointPows defines n. The interval distance is constant and equal for all intervals.
For information on the latency of the operator, see Table 44, 'Individual Latencies of the Operators in Library Memory'.
Each interval is described by a start base point and an end base point. The start base point defines the output value for the 1st interval step. The end base point defines the theoretical value for the end point of the interval that cannot be reached which is equal to the start base point of the next interval. All values inside the interval are approximated linearly. The end base point and the start base point of the consecutive interval have the same X-coordinate, i.e. there is no interval steps in-between.
Base points values for each interval in the KneeLUT can be defined individually. It is possible to define a discontinuous function over the entire output range. However, the sub functions inside each interval are linear with a gradient/slope defined through the start and the end base points. All start base points belong to the intervals. All end base points are excluded from the interval and can never be reached by the linear approximation.
All base points are normalized to the maximal representable value at the output of the operator, i.e. to
 .
All start base points will be in the range from 0 to 1.
Zero corresponds to the smallest representable value on the output.
In this version of KneeLut it is equal to 0 because the operator supports only unsigned values.
One represents the maximal representable value on the operator output, i.e.
.
All start base points will be in the range from 0 to 1.
Zero corresponds to the smallest representable value on the output.
In this version of KneeLut it is equal to 0 because the operator supports only unsigned values.
One represents the maximal representable value on the operator output, i.e.
 .
All end base points can exceed the range of 0 to 1 to allow the last value included in the interval to be mapped to the
highest and lowest numbers,
i.e. to 0 and 1.
This implies that the end base point might be larger than 1 or smaller than 0. Using the same scaling technique as for
the start base points,
the end points must be scaled to
.
All end base points can exceed the range of 0 to 1 to allow the last value included in the interval to be mapped to the
highest and lowest numbers,
i.e. to 0 and 1.
This implies that the end base point might be larger than 1 or smaller than 0. Using the same scaling technique as for
the start base points,
the end points must be scaled to
 .
.
Let's have a look at two examples to illustrate the behavior of the operator.
-
Identity
The first function of the KneeLUT is the identity. Suppose the following parameters of our KneeLUT:
- BasePointPows = 2
- Input Bit Width = 4
- Output Bit Width = 5
Thus we have to define four start base points and four end base points. For identity we define:


These values are determined by:

where x is the base point index.
The following plot shows these base points. Start base points are marked with a red square and end base points are marked by a magenta circle. Moreover, a line is plot to illustrating the linear functions of the intervals.
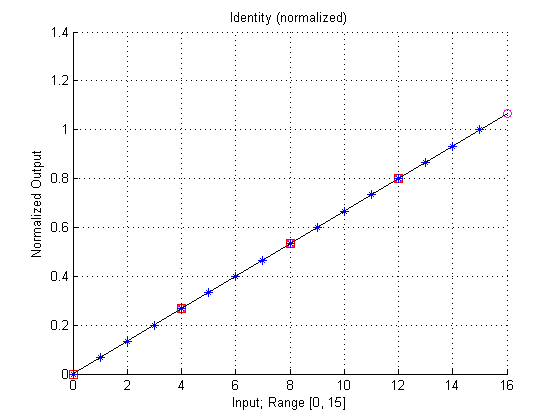
The plot also shows the approximated values of the output (blue stars). Base points are normalized, i.e. a 0 is output value 0 and 1 is output value
 .
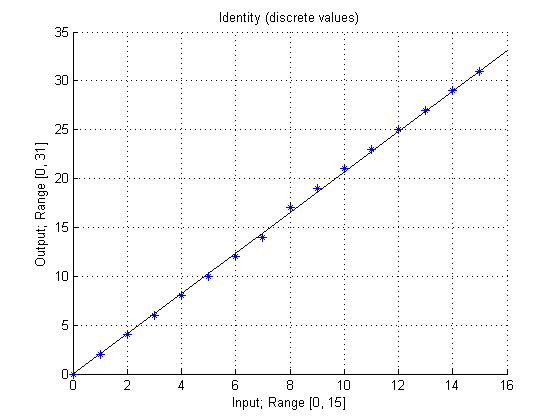
The following plot shows the actual used lookup table with the given base points.
As can be seen, the values are rounded to the next integer values.
.
The following plot shows the actual used lookup table with the given base points.
As can be seen, the values are rounded to the next integer values.
The lookup table will calculate the following values:
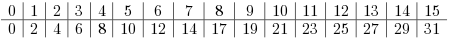
-
Discontinuous Function
In the next example we take a look on a discontinous function. Let's assume the same KneeLUT parameters as give in the first example. This time, the base points are not defined by a function:
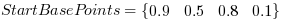
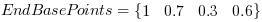
Again, the following plot shows these base points. Start base points are marked with a red square and end base points are marked by a magenta circle. Moreover, a line is plot to illustrating the linear functions of the intervals.
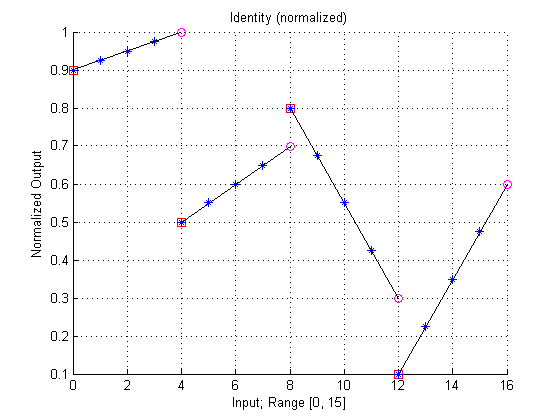
The plot also shows the approximated values of the output (blue stars). Again, the plot is normalized to 1.
The following plot shows the actual used lookup table with the given base points. As can be seen, the values are rounded to the next integer values.
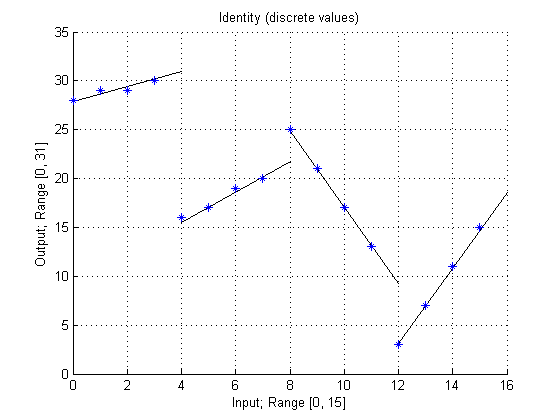
The lookup table will calculate the following values from the given base points:
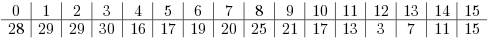
These values can be calculated by using the slope m(x) and the offset b(x) of each interval
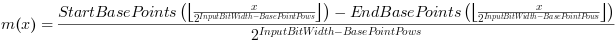
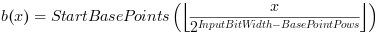
The result LUT(x) is then
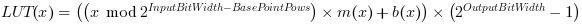
![[Warning]](../common/images/admon/warning.png) |
Approximated Values out of Range |
|---|---|
|
If the approximated values are out of the available output range, the operator will not clip them to the maximum or minimum possible value. Values are undefined. |
Operator Restrictions
-
The following constraint is given:
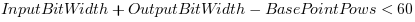
| Property | Value |
|---|---|
| Operator Type | O |
| Input Link | I, image data input |
| Output Link | O, data input |
| Link Parameter | Input Link I | Output Link O |
|---|---|---|
| Bit Width | [1, 64] | [1, 60] |
| Arithmetic | unsigned | as I |
| Parallelism | any | as I |
| Kernel Columns | 1 | as I |
| Kernel Rows | 1 | as I |
| Img Protocol | {VALT_IMAGE2D, VALT_LINE1D, VALT_PIXEL0D} | as I |
| Color Format | VAF_GRAY | as I |
| Color Flavor | FL_NONE | as I |
| Max. Img Width | any | as I |
| Max. Img Height | any | as I |
| BasePointPows | |
|---|---|
| Type | static parameter |
| Default | 6 |
| Range | [1, 60 - InputBitWidth + OutputBitWidth] |
|
This parameter defines the number of base points for the KneeLUT according to the following formula: NumberOfBasePoints = 2 ^ BasePointsPows. The step size is the parallelism. |
|
| StartBasePoints | |
|---|---|
| Type | dynamic/static read/write parameter |
| Default | identity function |
| Range | any |
|
This field parameter defines a set of normalized 2^BasePointPows interval start base points. The points are normalized to the maximal representable value on the operator output. Learn on how to configure field parameters in 'Parameter Editing'. |
|
| EndBasePoints | |
|---|---|
| Type | dynamic/static read/write parameter |
| Default | identity function |
| Range | any |
|
This parameter defines a set of normalized 2^BasePointPows interval end base points. The points are normalized to the maximal representable value on the operator output. The normalized values can exceed the range from 0 to 1 to allow the last interval point to reach the maximal respectively the minimal representable value. |
|
The use of operator KneeLUT is shown in the following examples:
-
Examples - Shows the use of a lookup table for 16 Bit input and output data. For 16 bit a Knee LUT has to be used due to the limited block RAM resources.

 Prev
Prev