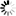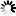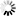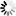A combination of image rotation and translation in 2 dimensions with coordinates x and y can be expressed with:
Here x' and y' are the coordinates in the target image. The rotation angle is
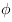 and
and
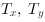 are the translation parameters in x and y direction.
The inverse translation and rotation is then:
are the translation parameters in x and y direction.
The inverse translation and rotation is then:
And therefore the coordinates in the source image are calculated as:
For a VA design we need the inverse transformation for coordinate calculation due to target-to-source mapping.
Scaling of the coordinates can be realized by multiplication with constants 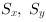 for x and y direction.
for x and y direction.
Optical distortion appears when the magnification of an object changes with distant to optical axis. The image has then
barrel or pincushion shape. For the VA design
we use a polynomial ansatz according to [Par09]. The distorted coordinates
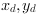 are calculated from undistorted coordinates
are calculated from undistorted coordinates
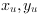 as:
as:
The coordinates are relative to the optical center of distortion. The parameters 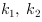 are the distortion coefficients. Some open source programs e.g. OpenCV give the possibility to calculate those parameters
with calibration images [Ope16a].
For all
are the distortion coefficients. Some open source programs e.g. OpenCV give the possibility to calculate those parameters
with calibration images [Ope16a].
For all 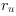 a lookup-table with the correction parameters
a lookup-table with the correction parameters
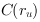 can be calculated with a Matlab program. You can find it under
\examples\Processing\Geometry\GeometricTransformation\LUTDistortionCorrection.m. With this table all distorted coordinates
can be calculated by simple multiplication with the undistorted coordinates.
can be calculated with a Matlab program. You can find it under
\examples\Processing\Geometry\GeometricTransformation\LUTDistortionCorrection.m. With this table all distorted coordinates
can be calculated by simple multiplication with the undistorted coordinates.
This trapezoidal distortion appears when the camera is not placed perpendicular to the object to be filmed.
With a 3x3 transformation matrix M with elements
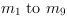 this effect can be corrected as
[Ope16b]:
this effect can be corrected as
[Ope16b]:
Please notice that we perform here inverse correction due to target-to-source mapping. The variables
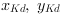 and
and
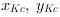 are the Keystone distorted and
Keystone corrected coordinates respectively.
are the Keystone distorted and
Keystone corrected coordinates respectively.
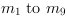 can be calculated with
OpenCV functions [Ope16b].
can be calculated with
OpenCV functions [Ope16b].

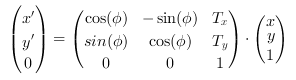
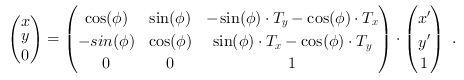
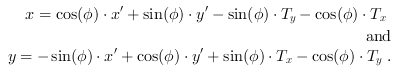
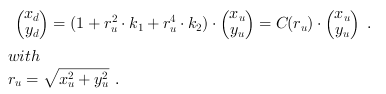
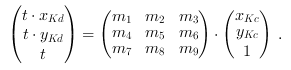
 Prev
Prev