| Brief Description | |
|---|---|
|
File: \examples\Processing\Geometry\ImageMoments\ImageMoments.va |
 |
|
Default Platform: mE5-MA-VCL |
|
|
Short Description Calculates the image moments orientation and eccentricity for the incoming images. |
|
Moments in image processing are average values from the single pixels` intensities of an image. With this moments physical properties like orientation, eccentricity, the area or the centroid of an object in the image can be identified.
The orientation 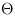 of an object is defined as
[Bur06]:
of an object is defined as
[Bur06]:
with the central moments of second order:
with definition
The centroid is
and the raw moments
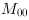 corresponds to the area of an object.
Here g(x,y) is the greyscale function for digital greyscale images.
corresponds to the area of an object.
Here g(x,y) is the greyscale function for digital greyscale images.
The eccentricity e of an object can be calculated with [Bur06]
The results of the eccentricity are in a range between 0 (round object) and 1 (elongated object).
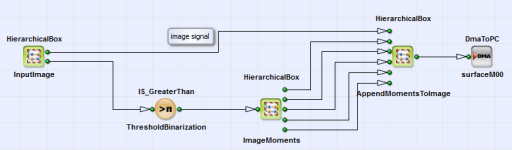
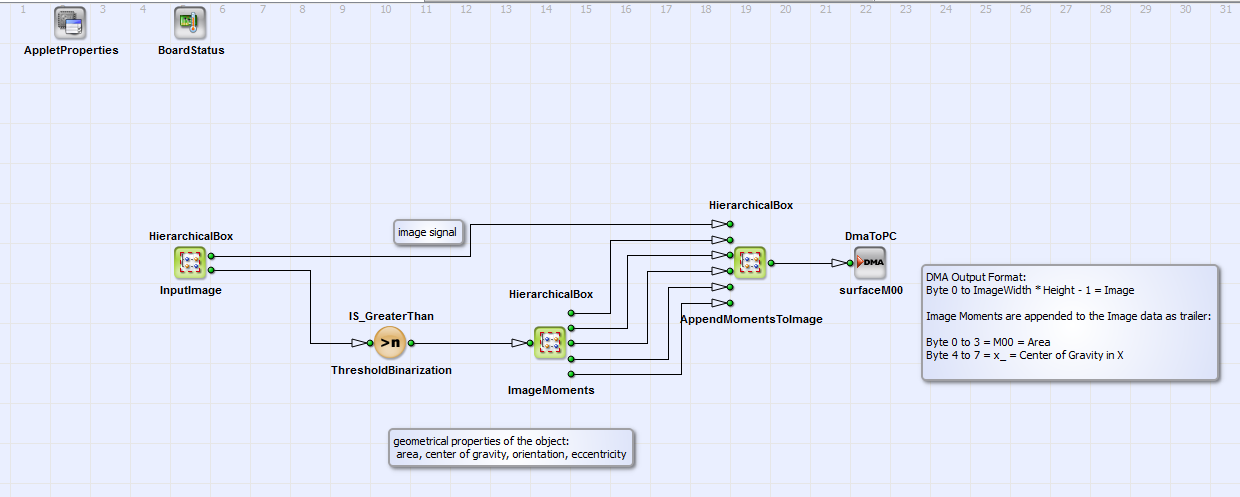
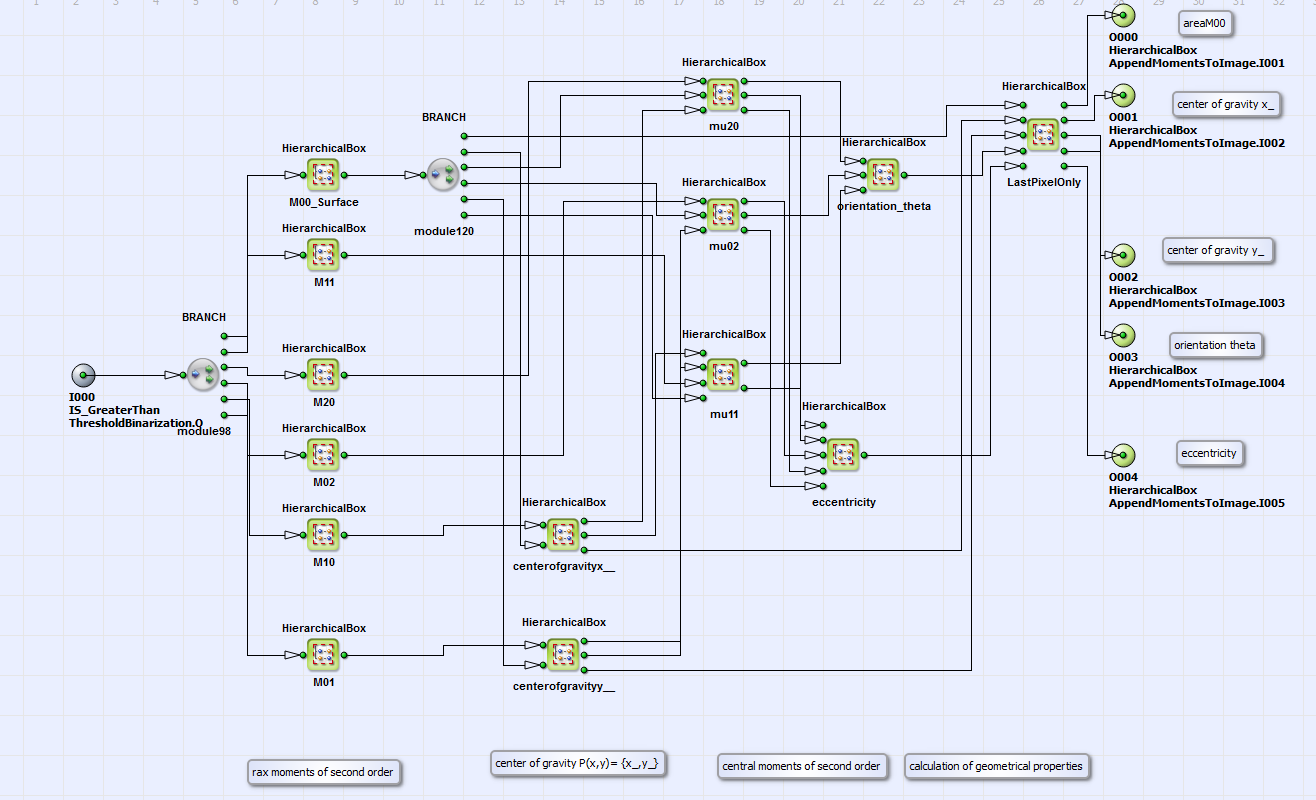
In VisualApplets a design is implemented with the original image and geometric properties like the area, the center of gravity, the orientation and the eccentricity of an object as output. You can find the example under \examples\Processing\Geometry\ImageMoments\ImageMoments.va. A parallelism of 4 was chosen for calculation. In Figure 346, 'Basic design structure' the structure of the design with comments is shown.
Geometric properties area, center of gravity, orientation and eccentricity of a greyscale image are calculated via moments
(HierarchicalBox: ImageMoments).
These properties are appended to the original camera image (AppendMomentsToImage).
In Figure 347, 'Content of ImageMoments' the content of the HierarchicalBox ImageMoments is shown. The raw moments
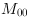 (which corresponds to the area of an object),
(which corresponds to the area of an object),
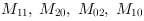 and
and 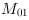 , as well as the center of gravity
, as well as the center of gravity 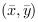 and the central moments
and the central moments 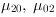 and
and 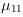 are implemented according to the formulas given above. Finally the geometric properties orientation
are implemented according to the formulas given above. Finally the geometric properties orientation
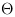 of the main axis and eccentricity e
of an image object are calculated from these results.
of the main axis and eccentricity e
of an image object are calculated from these results.
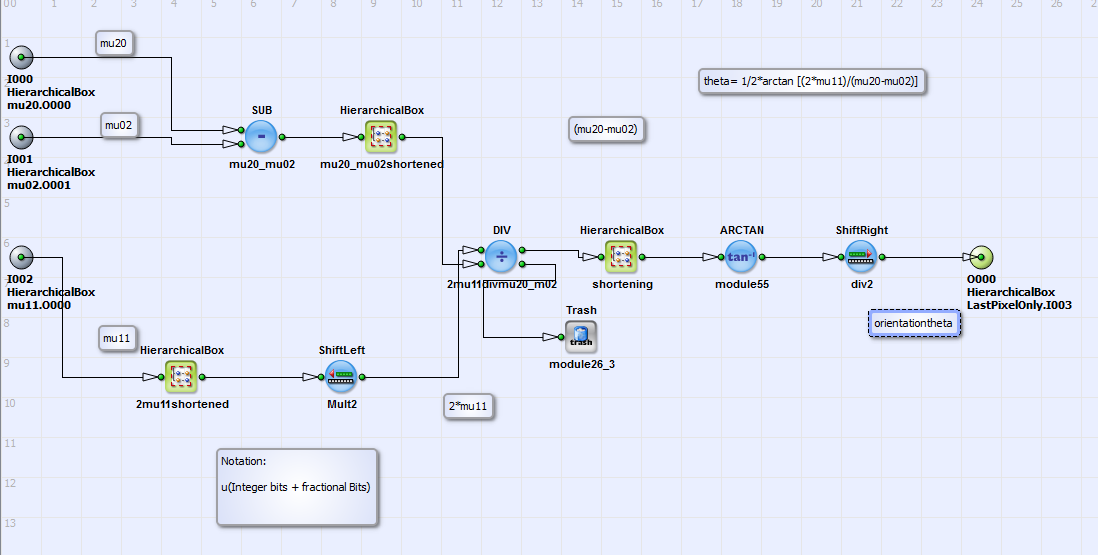
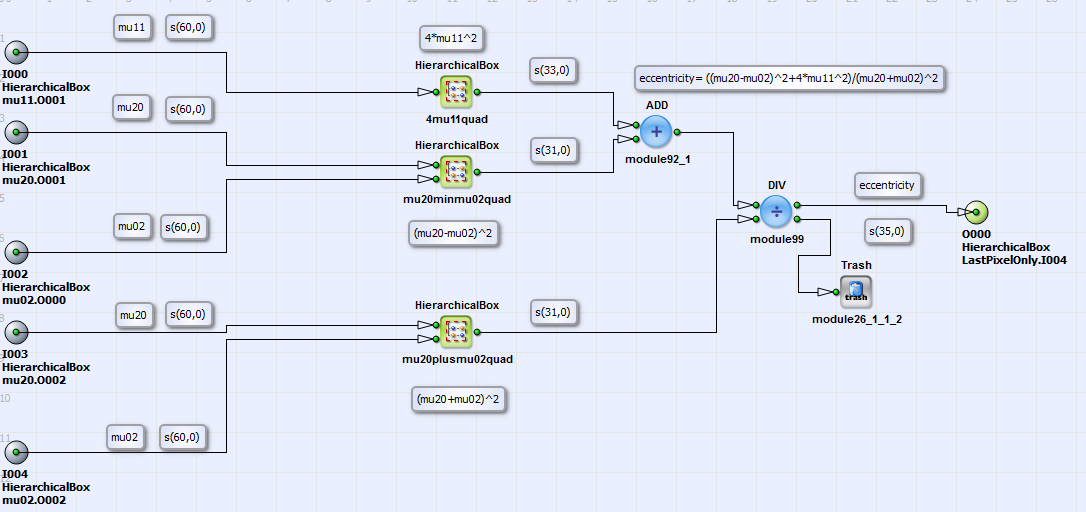
In Figure 348, 'Content of the HierarchicalBox orientation_theta' and Figure 349, 'Content of the HierarchicalBox eccentricity' the contents of the HierarchicalBoxes orientation_theta and eccentricity
together with inserted comments on the single operation steps are shown. The orientation 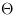 and eccentricity e are calculated by using the values of
and eccentricity e are calculated by using the values of
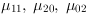 according to Equation 24 and
Equation 29.
A resolution of R=7 is chosen for the input signal to the ARCTAN operator.
according to Equation 24 and
Equation 29.
A resolution of R=7 is chosen for the input signal to the ARCTAN operator.
Comment: During implementation of the orientation of Θ it showed, that limitation to 12 bits maximum input signal of the ARCTAN function can be a problem for calculation of accuracy and resolution: for example the image of an ellipse with orientation Θ= 44.07° (result of moment implementation with MATLAB) was analyzed. The 25 bit input signal for the ARCTAN function has to be limited to 12 bits. With resolution of R= 8 bits the implementation in VisualApplets has result 41.43°; with R=7 bits the result is 43.21° (with resolution for small angles of 0.2°) and with R= 6 it is 44.07° (with resolution for small angles of 0.45°). As an result we found that with high resolution (R= 8 bit) the maximum angle of calculation is smaller than the true angle of orientation, due to bit depth limitation. With smaller resolution R the result of calculation improves for big angles but has as an consequence smaller accuracy in the range of small angles. The problem can be solved by using a Lookup table instead of ARC TAN operator.

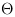
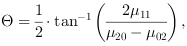
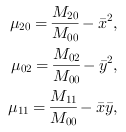
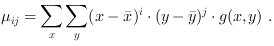
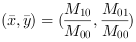
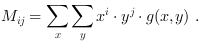
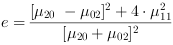
 Prev
Prev